∫(6xy²-y^3)dx (6x²y-3xy²)dy
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/18 08:55:42
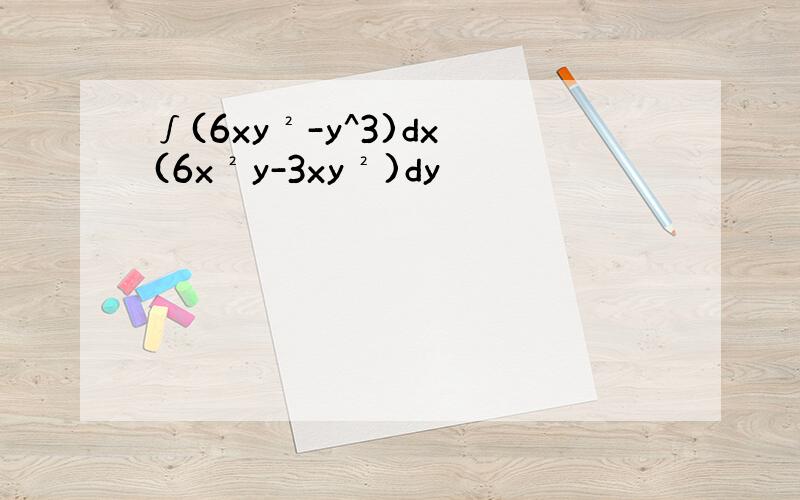
解析2xdx+ydx+xdy+3y²dy=0(2x+y)dx+(x+3y²)dy=0(2x+y)dx=-(x+3y²)dydy/dx=(2x+y)/-(x+3y²
3xy是3x原式=(x-3y)(x+2y)+3x+y+2十字相乘x-3y2×x+2y1所以原式=(x-3y+2)(x+2y+1)
(1)(xy+x^3y)dy-(1+y^2)dx=0(xy+x^3y)dy=(1+y^2)dx分离变量整理得:y\(1+y^2)dy=1\x(1+x^2)dx整理:y\(1+y^2)dy=1\x-x\
令z=1/x,则dx=-x²dz代入原方程得(x²y³+xy)dy=-x²dz==>dz/dy+y/x=-y³==>dz/dy+yz=-y³
方程两边同时对x求导得2yy'-3(y+xy')=0整理化简得y'=3y/(2y-3x)即dy/dx=3y/(2y-3x)
(6xy^2-y^3)dx+(6x^y-3xy^2)dy=d(3x^y^-xy^3),∴原式=(3x^y^-xy^3)|,=(9x^-7x)|=9*7-7=56.再问:原式==(3x^y^-xy^3)
(3x²+6xy²)dx+(6x²y+4y²)dy=0分组得:3x²dx+(6xy²dx+6x²ydy)+4y²dy=0
令y/x=u,dy=u+xdu,原方程化为:u+xdu/dx=x/(u^2)+u,即du/dx=1/(u^2)通解为:y=x*[(3x+3c)^(1/3)]
∵dy/dx=(x+y^3)/(xy^2)==>xy^2dy=(x+y^3)dx==>y^2dy/x^3=dx/x^3+y^3dx/x^4(等式两端同除x^4)==>d(y^3)/(3x^3)+y^3
别人一般问一道题,你一下子5道?我给你个提示:1.所有5道题全部可以化成y'=f(y/x)的形式.比如5::y’=√(1-y^2/x^2)+y/x2.设y/x=uy=xuy'=u+xu',代入:u+x
令z=1/x,则dx=-x²dz代入原方程得(x²y³+xy)dy=-x²dz==>dz/dy+y/x=-y³==>dz/dy+yz=-y³
就是把这dydx转为求导前的式子,然后再求导一遍验证一下对错.再问:就是算到最后有个积分搞不出来。求过程。
答案:2.过程不详述了.这个积分是跟路径无关的,因为原函数是一个函数(3xxyy-xyyy)的全微分.在这种情况下,积分值等于原函数在起始点值的差.
很明显这是个全微分方程用积分,从(0,0)沿x轴积到(x,0),再沿与y轴平行的直线积到(x,y)u(x,y)=∫(0,x)3x^2dx∫(0,y)6x^2y+4y^2dy=x^3+3x^2y^2+4
原式=-x²y+2xy²+2x²y²-4xy³-3x³+27x³y-18x²y²+2x²y-18x&
(3X²+6xy²)dx+(6x²y+4y²)dy=03X²dx+4y²dy+(6xy²dx+6x²ydy)=0dx&s