F（x,y)=(1-e^-3x)(1-e^-5y) x,y≥0

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/14 02:55:12

F（x,y)=(1-e^-3x)(1-e^-5y) x,y≥0
求：概率密度f（x,y)
我的解：对F求导把原式展开,1- e^-5y -e^-3x -e^-(3x+5y) 然后对其中每一项分别求导
0+5e^-5y+3e^-3x+?最后一项-e^-(3x+5y)怎么求导
答案是3e^-3x * 5e^-5y
=15e^-3x-5y.

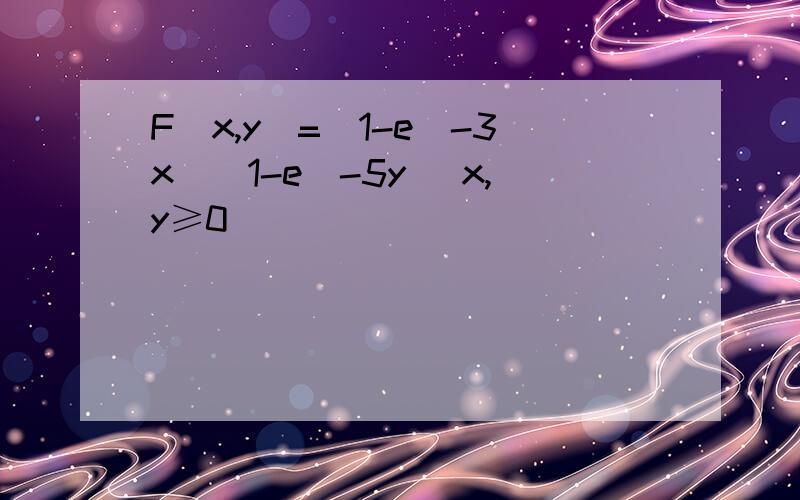
F（x,y)=(1-e^-3x)(1-e^-5y)
f(x,y)=Fx(x,y)=[(1-e^-3x)']·[(1-e^-5y)']
=[-(-3x)'·e^-3x]·[ -(-5y)'·e^-5y]
=3·e^-3x·5·e^-5y
=15·e^-3x·e^-5y
=15·e^（-3x-5y）；
####

大学概率：设随机变量（X,Y）具有分布函数F（x,y）=1-e^(-x)-e^(-y)+e^(-x-y),x>0,y>o 大学函数表达式已知,f(0)'=1,f(x+y)=f(x)*(e^y)+f(y)*(e^x)求 f(x)的表达式. 设二维连续性随机变量(x,y)的分布函数为F(x,y)=(1-e^-3x)(1-e^-5y),x>0,y>0,求(X,Y y'e^(x-y)=1通解? 设二维随机变量(X,Y)的概率密度f(x,y)=1/2(x+y)e^-(x+y),x>0,y>0；=0 ,其他设随机变量x ,y x相互独立,且x~u[0,3],e(1/3),则x,y 的联合概率密度函数f（x,y)=? 高数题求微分方程通解.y''-3y'+2y=e^x(1+e^2x) y=e^x+e^-x/(e^x-e^-x) [e^(x+y)-e^x]dx+[e^(x+y)-e^y]dy=0求通解极限和微分方程的问题f(x)=[(1+x)^0.5-e]/x x趋向于0[(3x^2+y^2)/y^2]dx-[(2x^ 求微分方程的通解 {[e^(x+y)]-e^x}dx+{[e^(x+y)]+ey}dy=0 答案是（e^x+1)（e^y 设f(x,y)= e^-sinx (x+2y),fx'(读作f次x)(0,1)=