如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2 BD,DF垂
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/12 01:01:24
如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2 BD,DF垂直AB于F.
如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2 BD,DF垂直AB于F.求证:CD=DF
请不要用到“等腰三角形的性质”只用“全等三角形和角平分线性质”!
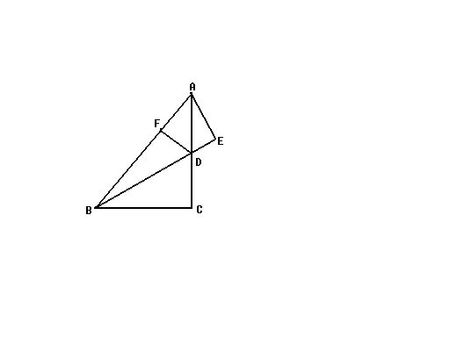
如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2 BD,DF垂直AB于F.求证:CD=DF
请不要用到“等腰三角形的性质”只用“全等三角形和角平分线性质”!


证明:延长AE与BC的延长线交于点G
∵∠ACB=90
∴∠ACG=∠ACB=90,∠CBD+∠CDB=90
∵AE⊥BD
∴∠BEA=∠BEG=90
∴∠CAG+∠ADE=90
∵∠CDB=∠ADE
∴∠CBD=∠CAG
∵AC=BC
∴△ACG≌△BCD (ASA)
∴AG=BD
∵AE=1/2BD
∴AE=1/2AG
∴AE=GE,E是AG的中点
∴BE垂直平分AG
∴AB=GB
∴△ABE≌△GBE (SAS)
∴∠ABE=∠GBE
∵DF⊥AB
∴CD=DF (角平分线性质)
∵∠ACB=90
∴∠ACG=∠ACB=90,∠CBD+∠CDB=90
∵AE⊥BD
∴∠BEA=∠BEG=90
∴∠CAG+∠ADE=90
∵∠CDB=∠ADE
∴∠CBD=∠CAG
∵AC=BC
∴△ACG≌△BCD (ASA)
∴AG=BD
∵AE=1/2BD
∴AE=1/2AG
∴AE=GE,E是AG的中点
∴BE垂直平分AG
∴AB=GB
∴△ABE≌△GBE (SAS)
∴∠ABE=∠GBE
∵DF⊥AB
∴CD=DF (角平分线性质)
如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2 BD,DF垂
如图,在△ABC中,∠C=90°,AC=BC,D是AC上的一点,AE⊥BD交BD的延长线于E,且AE=1/2BD,DF⊥
在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2BD,DG⊥AB于F
如图,△ABC中,AC=BC,∠CB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=1/2BD,求证:B
如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=二分之一BD.求
在三角形ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BO交BD的延长线与E,且AE=1/2BD,DF⊥AB
在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BC交BD的延长线於E,且AE=二分之一BD,DF垂直AB
在三角形ABC中,角C=90°,AC=BC,D是AC上一点,AE垂直BD交BD的延长线于E,且AE=BD的一半,DF垂直
如图△ABC中AC=BC ∠ACB=90°D是AC上一点,AE⊥BD交BD延长线于E且AE=二分之一BD求证BD是∠AB
如图,三角形ABC中角C=90度,AC=BC,D是AC上的一点,AE垂直BD交BD的延长线于点E,且AE=二分之一BD.
如图 三角形ABC中 AC=BC 角ACB=90° D是AC上一点 且AE⊥BD 交BD的延长线于E,BD是角ABC的平
如图 三角形ABC中 AC=BC 角ACB=90° D是AC上一点 且AE⊥BD 交BD的延长线于E 又AE=&frac